Ergosphere
This article should be divided into sections by topic, to make it more accessible. (September 2023) |
The ergosphere is a place just outside the event horizon of a black hole. Its name was given by Remo Ruffini and John Archibald Wheeler in 1971 and is gotten from the Greek word ἔργον (ergon), which means "work". It got its name because it is possible to get energy and even mass from this place.
In this place, it's impossible to stay in one place because of "frame-dragging." According to general relativity, anything that spins will twist the spacetime around it. This is frame dragging. So, near a rotating black hole, things start spin around it. For a spinning black hole, frame-dragging is so strong that to stay in one place, you'd have to move backward faster than the speed of light, which is impossible.[1]
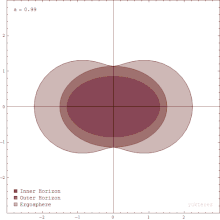
Now, this ergosphere isn't just a simple circle; it has a bit of a shape. It's kind of like a big, flattened ball. Think of it as an oblate spheroid, sort of like a pumpkin. At the top and bottom of the black hole, it touches the event horizon, but as you move toward the equator (the middle part), it goes out farther.
The size of this ergosphere depends on how fast the black hole is spinning. If it's spinning just a bit, the ergosphere is more round. But if the black hole is spinning very fast, the ergosphere starts looking more like a stretched pumpkin.
The edge of the ergosphere at the equator has the same size as the Schwarzschild radius of a black hole. And at the poles, it can be even smaller, like just half the Schwarzschild radius, especially for a super-fast-spinning black hole.
If something is inside the ergosphere, it can still escape from the black hole. But with more energy than when it went in. And we could get energy from it through the Penrose process. [2]
References
[change | change source]- ↑ Carroll, Sean M. (1973). Spacetime and geometry: an introduction to general relativity (Nachdr. ed.). San Francisco Munich: Addison-Wesley. ISBN 978-0-8053-8732-2.
- ↑ Griest, Kim (26 February 2010). "Physics 161: Black Holes: Lecture 22" (PDF). Archived (PDF) from the original on 2012-04-03. Retrieved 2011-10-19.
