Quadratic function

A quadratic graph with two real answers and no complex answers. Other quadratic graph have no real answers and 2 complex answers.

In algebra, a Quadratic function is a function that contains an expression where its degree (the highest exponent it has) is 2, which means that it is quadratic (See etymology). Its single-variable standard form isː

$f(x)=ax^{2}+bx+c$

Where $a$, $b$ and $c$ are all constants and $a$ ≠ 0.

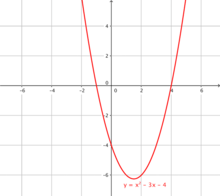
When such a function gets plotted on a graph where $f(x)=y$, a curve that extends infinitely called a parabola will appear.

When a quadratic function is set equal to zero, then it turns into a quadratic equation. The answers to the equation are where the function crosses the $x$-axis.

Etymology

The word quadratic comes from the Latin word quadrātum ("square"). This is because of the presence of a number (which is$x^{2}$ in the standard form) that is the result of squaring its square root ($x\times x=x^{2}$).